Home 
  OpticsPOD
  What's New 
  Rays & Shadows
  Water Droplets
  Rainbows
    Not a rainbow!
    Primary Bow
      Raindrop Rays
      Rainbow Cone
      Low & High Bows
      Drop size
      Colours
    Secondary Bow
    A's Dark Band
    Other Orders
    Supernumeraries
    Red Bows
    Rainbow Wheel
    Dew Bow
    Sea Spray Bow
    Glass Bead Bows     Reflection Bows
    Twinned Bows
    Cloud Bows
    Moon Bows
    Image Gallery
    Simulators
  Ice Halos
  High Atmosphere
  Links & Resources
  Search - Index



                 

123456789012345678
   Through a drop brightly - light rays


      


  
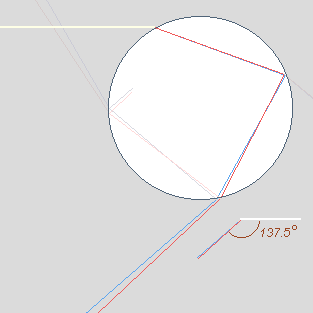
Rays** reflected once inside raindrops make the primary. Its colours are produced by the two refractions as the rays enter and leave. Rays are deviated back towards the incoming sunlight to form a bow appearing opposite the sun. The rays drawn in lighter tones form the "zero order glow", the secondary and higher order bows.

One internal reflection produces the primary bow.  
   
  Mouse over the slider to see the ray paths. Rays close to the drop centre are deviated almost 180º back on themselves. Rays further from the centre are deviated less and less until the deviation reaches a minimum (about 137.5º for deep red light). This is the "angle of minimum deviation" or "rainbow angle". The deviation increases once more as the entrance ray approaches the drop rim .
  

Light is deviated into a whole range of angles
  Rays cluster strongly around the rainbow angle, test it with the mouse, and so the bow is at its brightest at that angle. Rays near the rainbow angle form the bow's bright outer edge.
   		  Minimum deviation angle

Red light is refracted less than blue and its minimum deviation angle is less. Red is therefore on the outside of the primary bow.
  
Colour separation

Rays deviated through larger angles make the sky brighter inside the primary. The brighter sky is colourless because at those angles the colours strongly overlap.
  
Bright sky inside the bow
  No light is deviated through angles smaller than the minimum deviation angle and the sky is therefore darker beyond the outer edge of the primary bow.
  
  		  Outside the bow is dark
  * 
   		Raindrops are never the tear shaped objects beloved of illustrators. Small raindrops are kept strongly spherical by surface tension forces. Larger drops are sometimes flattened by air resistance as they fall and they may even oscillate or wobble. Even small departures from sphericity destroy a rainbow or possibly cause some odd effects.

   Spheres not teardrops
  ** 
   		Ray paths are something of a fiction and geometric optics is incapable of explaining many aspects of rainbows. However, when raindrops are a millimetre or so in diameter the straight line rays are a reasonable approximation to some aspects of how light behaves.

   Don't take ray paths too seriously
  ***  Deviations are traditionally measured from the direction of the incoming sunlight. The deviation angle for red rays forming the edge of the primary bow is about 137.5º. The centre of a rainbow is directly opposite the sun (a deflection angle of 180º). The radius of the red edge of the primary is therefore 180-137.5 = 42.5º
   		  Deviation angles
  ****  The ray paths are accurately computed for wavelengths of 400 and 750 nm passing through a water drop at 0 Celsius.
   		  Calculation

 

 

 

Rays through a raindrop.

Rainbow forming raindrops are spheres*. The primary bow is formed by rays reflected once inside them.

Rays emerge at many angles. Those deviated least are the most numerous. They form the outer coloured edge of the bow.